New technology emerges to make fair dice in any shape, including cats and dragons

A joint research team from Carnegie Mellon University, NVIDIA, and Adobe has published a paper on how to predict the orientation in which
Putting Rigid Bodies to Rest
(PDF file) https://hbaktash.github.io/files/rolling_dragons_paper.pdf
In the past, to calculate which side of a die will come to rest facing up when it is rolled, the rolling of the object was simulated multiple times on a computer and statistics were taken. However, this required an enormous amount of calculation time and effort, and there were problems with accurate predictions, especially for objects with complex shapes.
The research team therefore focused on a method of calculating the probability of which surface an object will come to rest on, without performing any physical simulations, using only the geometric properties of the object's 'shape' itself as a clue.
The basis of this method is a simple law of physics: 'When an object rolls, it loses momentum and eventually comes to rest at its lowest center of gravity, i.e., in its most stable state.' The research team considers the height of the center of gravity of an object when it is in various orientations, and mathematically analyzes how this height changes depending on the orientation of the object.
First, consider the smallest convex shape that completely covers the outside of the object. Next, use a special method called the Gaussian map to organize the orientation of the object when each face, edge, and vertex of this convex shape touches the ground as points and lines on the surface of a sphere. This makes it possible to capture any orientation of the object as a position on this sphere.
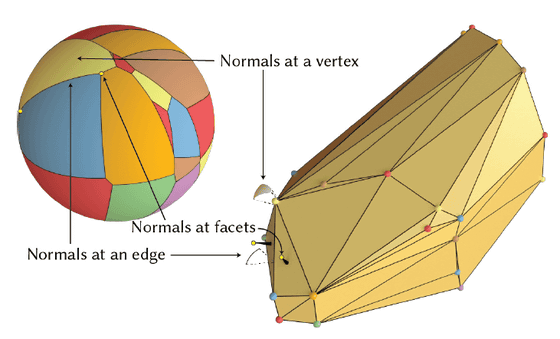
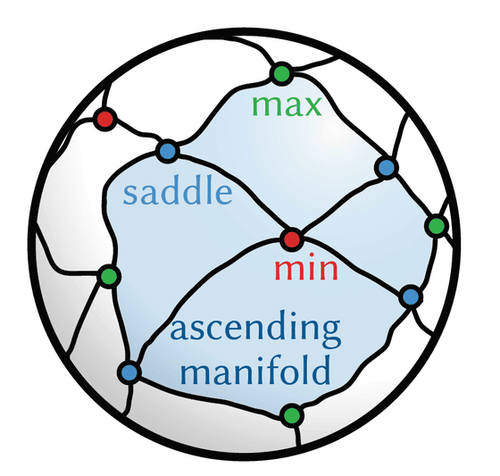
The height of the center of gravity of an object when it is in a particular orientation is represented as a 'map' on the sphere. The object changes direction on this 'map of center of gravity height' as if it were rolling down the steepest slope. By following this 'rolling path,' we can predict which stable depression, or stationary surface, the object will eventually reach.
When tracing this path, the rules for how the direction changes depend on whether the objects are connected at a vertex, an edge, or a face. For example, if they are connected at an edge, the specific movement is classified and calculated: will the edge roll to the next vertex like a 'wheel,' or will it fall flat onto the adjacent face?
Finally, this 'height map of the center of gravity' is analyzed as a whole, and the 'area of influence' is calculated, which is the range of stable resting surfaces from which the wave will flow and from what initial direction. The proportion of this area is the probability that the wave will come to rest on that surface. This analysis uses a method called the '
The series of calculations is so fast that, for example, the six resting orientations of a pig-shaped toy dice and their probabilities can be calculated in just 3 milliseconds.

What makes this 'rolling prediction' calculation method so great is that it is not only fast, but also has the mathematical property of being 'differentiable.' This means that it is possible to calculate how 'if the shape of an object is slightly changed, how will the probability of it coming to rest change?' The research team argues that by taking advantage of this property, they have made it possible to 'inversely design' rigid bodies.
Inverse design involves setting a goal, such as 'I want to make a fair three-sided die in the shape of a cat, with each side having a 1/3 probability of appearing,' or 'I want to make a special 11-sided die that has the same probability of appearing when two regular dice are rolled,' and then the computer can automatically design the shape of an object to have the probability distribution of the goal.
In this design process, we start with a rough initial shape. We then define an 'energy function' that quantifies the deviation between the 'current rest probability of each face' and the 'target probability.' The computer calculates the direction in which the value of the energy function decreases so as to minimize this deviation, and gradually corrects the positions of the vertices of the object accordingly. By repeating this correction, the shape will automatically approach the target probability distribution.
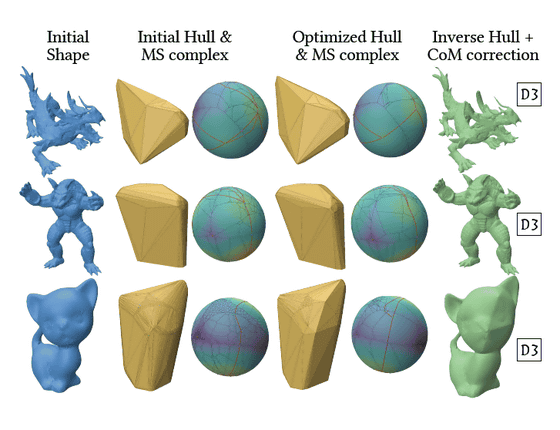
The design does not just match the probability, but also takes into account requests for appearance and physical stability, such as 'the surface that stops stably should be as flat and wide as possible' and 'avoid multiple surfaces being stable in almost the same direction.' This makes it possible to create more practical and beautiful designs.
The research team used a 3D printer to create special dice in the shape of a cat or armadillo, and rolled them hundreds to thousands of times to collect statistics. As a result, in many cases, the calculated predicted probability was in good agreement with the experimental results obtained by actually rolling them. This shows that this geometric approach captures real phenomena very well, despite being based on the simplifying assumption of ignoring momentum.

In the movie below, you can see the research team actually rolling the dice printed by a 3D printer.
Tired of boring old dice? Roll some dragons and armadillos! - YouTube
Of course, if the ball is rolled very fast or if the object bounces multiple times, the effect of momentum will be greater and the prediction may differ from the actual result. In addition, there are other issues that remain to be addressed, such as the assumption of the initial direction in which the ball starts to roll and the manufacturing limitations of accurately creating very detailed and complex shapes using a 3D printer.
However, the research team said that in the future, the technology could be used in a variety of fields, not just for dice used in games, such as placing parts in the correct orientation on automated industrial assembly lines or evaluating the stability of robots gripping objects.
Related Posts:







