What does the 'bilinear interpolation' algorithm that enlarges and reduces images do?

When enlarging or reducing an image, if the image is simply processed as it is, the image quality will become rough. Therefore, an algorithm is needed to smooth the image and enlarge or reduce it while maintaining a relatively clean image quality. Bart Wronski, who works as a graphics software engineer at NVIDIA Research, explains what one such algorithm, 'bilinear interpolation,' is.
Bilinear texture filtering – artifacts, alternatives, and frequency domain analysis | Bart Wronski
First, Wronski said, 'Most people have the image that pixels are small squares lined up on a screen, but this is just a superficial appearance. A pixel is essentially a sample value at a spatial point, and does not have any extent or area.' The pixels that make up an image are numerical representations of information such as color and brightness.
'Simple enlargement of an image' means 'expanding the interval between consecutive points', so that expansion needs to be interpolated. How this interpolation is performed determines the quality of the enlarged image.

Bilinear interpolation works simply: when calculating the color data for a given point, it uses a
For example, to find the color of a point at coordinates (1.3, 2.6) in an image, check the colors of the four pixels surrounding this point: (1, 2), (1, 3), (2, 2), and (2, 3). Then, first perform horizontal linear interpolation between (1, 2) and (2, 2), and (1, 3) and (2, 3), then perform vertical linear interpolation between Y coordinates = 2 and 3 to determine the data for (1.3, 2.6). Since linear interpolation is performed twice (bi), it is called bilinear interpolation.
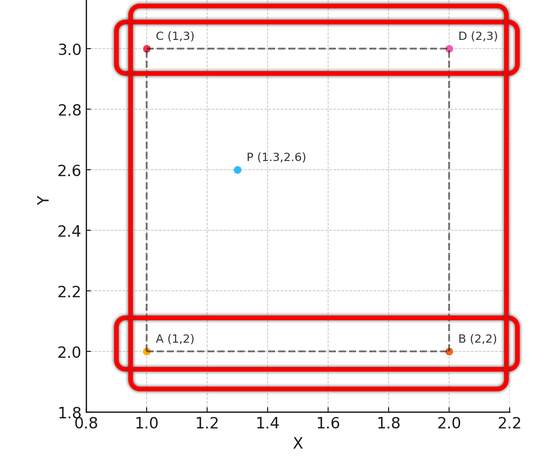
Bilinear interpolation is suitable for real-time processing because the calculations are simple, there is hardware support that can be executed with one instruction on a GPU, and it can be executed at a fairly low cost, explains Wronski. In addition, bilinear interpolation smoothly interpolates the values of four adjacent pixels, resulting in a natural and smooth image with less jagged and block-like image degradation.
However, while bilinear interpolation is fast and easy to use, it has some significant drawbacks, Wronski points out.
First, visually unnatural artifacts such as jagged edges and star patterns that appear when enlarging an image are likely to occur, especially in low-resolution textures and high-contrast images. This is due to the fact that the interpolation calculation is structured to multiply triangular weights vertically and horizontally, resulting in pyramidal patterns appearing on the image.

In addition, because human vision is sensitive to subtle changes in contrast, the interpolation result can produce illusory differences in light and dark known as 'Mach bands,' making what should be a smooth gradation appear stepped.

In addition, the effect of the interpolation is highly dependent on the fractional values of the coordinates, resulting in uneven processing results in which the sharpness or blurring varies from place to place across the image. These variations are easily perceived as 'flickering' or 'instability' in animations and dynamic zoom operations.
From the viewpoint of signal processing, bilinear interpolation changes the signal distribution, i.e. the contrast, depending on the position, resulting in localized blurring of the image. In addition, because it largely removes high-frequency components, it is easy to lose fine details, resulting in a loss of image clarity.
In addition, since the GPU has a specification that the center of the pixel is shifted by 0.5, if bilinear interpolation that does not correspond to this is used, the image will be displayed half a pixel off to the left and right, and there will be a misalignment problem, Wronski said. These problems directly affect the visual quality, so if they are not properly addressed, they can cause unintended visual degradation or bugs.
Since there are multiple definitions and implementation 'styles' of bilinear interpolation, Wronski emphasized that the most important thing is not which one is correct, but to unify the handling of coordinate systems and pixel grids in the framework and processing system being used. He recommended not blindly accepting libraries and code, but reimplementing the process yourself to maintain coordinate consistency, since the content may differ even if the same term 'bilinear interpolation' is used.
Wronski said that if higher quality is required, switching to bicubic interpolation or Lanczos filters , or sharpening after interpolation, is effective. He added, 'Bilinear interpolation is convenient and powerful, but if not used correctly it can cause serious problems in image quality and behavior. For this reason, it is essential to have a good understanding of how it works and how to handle coordinate systems, and to maintain consistency throughout the process.'
in Software, Posted by log1i_yk